Skip to contents

LaMa

A variety of latent Markov models (Mews, Koslik, and Langrock 2024), including hidden Markov models (HMMs), hidden semi-Markov models (HSMMs), state space models (SSMs) and continuous-time variants can be formulated and estimated within the same framework via directly maximising the likelihood function using the so-called forward algorithm (Zucchini, MacDonald, and Langrock 2016). Applied researchers often need custom models that standard software does not easily support. Writing tailored R code offers flexibility but suffers from slow estimation speeds. This R package solves these issues by providing easy-to-use functions (written in C++ for speed) for common tasks like the forward algorithm. These functions can be combined into custom models in a Lego-type approach, offering up to 10-20 times faster estimation via standard numerical optimisers. The development version now also allows for automatic differentiation with the RTMB package which drastically increases speed and accuracy.

The most important families of functions are

  • the forward family that calculates the log-likelihood for various different models,

  • the tpm family for calculating transition probability matrices,

  • the stationary family to compute stationary and periodically stationary distributions

  • as well as the stateprobs and viterbi families for local and global decoding.

Installation

You can install the released package version from CRAN with:

or the development version from Github:

# install.packages("devtools")
devtools::install_github("janoleko/LaMa")

Package documentation

To aid in building fully custom likelihood functions, this package contains several vignettes that demonstrate how to simulate data from and estimate a wide range of models using the functions included in this package.

HMMs, from simple to complex:

Other latent Markov model classes:

Introductory example: Homogeneous HMM

We analyse the trex data set contained in the package. It contains hourly step lengths of a Tyrannosaurus rex, living 66 million years ago. To these data, we fit a simple 2-state HMM with state-dependent gamma distributions for the step-lengths.

library(LaMa)
#> Loading required package: RTMB

head(trex, 3)
#>   tod      step     angle state
#> 1   9 0.3252437        NA     1
#> 2  10 0.2458265  2.234562     1
#> 3  11 0.2173252 -2.262418     1

We start by defining the negative log-likelihood function. This is made really convenient by the functions tpm() which computes the transition probability matrix via the multinomial logit link, stationary() which computes the stationary distribution of the Markov chain and forward() which calculates the log-likelihood via the forward algorithm.

nll = function(par, step){
  # parameter transformations for unconstrained optimisation
  Gamma = tpm(par[1:2]) # multinomial logit link
  delta = stationary(Gamma) # stationary HMM
  mu = exp(par[3:4])
  sigma = exp(par[5:6])
  # calculate all state-dependent probabilities
  allprobs = matrix(1, length(step), 2)
  ind = which(!is.na(step))
  for(j in 1:2) allprobs[ind,j] = dgamma2(step[ind], mu[j], sigma[j])
  # simple forward algorithm to calculate log-likelihood
  -forward(delta, Gamma, allprobs)
}

To fit the model, we define the intial parameter vector and numerically optimise the above function using nlm():

par = c(-2,-2,             # initial tpm params (logit-scale)
        log(c(0.3, 2.5)),  # initial means for step length (log-transformed)
        log(c(0.2, 1.5)))  # initial sds for step length (log-transformed)

system.time(
  mod <- nlm(nll, par, step = trex$step)
)
#>    user  system elapsed 
#>   0.372   0.010   0.383

Really fast for 10.000 data points!

After tranforming the unconstrained parameters to working parameters using tpm() and stationary(), we can visualise the results:

# transform parameters to working
Gamma = tpm(mod$estimate[1:2])
delta = stationary(Gamma) # stationary HMM
mu = exp(mod$estimate[3:4])
sigma = exp(mod$estimate[5:6])

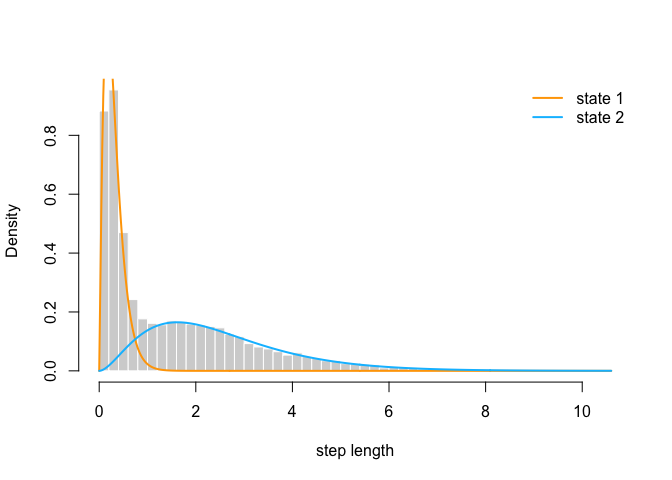
hist(trex$step, prob = TRUE, bor = "white", breaks = 40, main = "", xlab = "step length")
curve(delta[1] * dgamma2(x, mu[1], sigma[1]), add = TRUE, lwd = 2, col = "orange", n=500)
curve(delta[2] * dgamma2(x, mu[2], sigma[2]), add = TRUE, lwd = 2, col = "deepskyblue", n=500)
legend("topright", col = c("orange", "deepskyblue"), lwd = 2, bty = "n", legend = c("state 1", "state 2"))

Mews, Sina, Jan-Ole Koslik, and Roland Langrock. 2024. “How to Build Your Latent Markov Model - the Role of Time and Space.” arXiv Preprint arXiv:2406.19157.
Zucchini, Walter, Iain L. MacDonald, and Roland Langrock. 2016. Hidden Markov Models for Time Series: An Introduction Using R. Boca Raton: Chapman & Hall/CRC.