Penalised splines
Penalised_splines.RmdBefore diving into this vignette, we recommend reading the vignettes Introduction to LaMa, Inhomogeneous HMMs, Periodic HMMs and LaMa and RTMB.
This vignette explores how LaMa can be used to fit
models involving nonparameteric components, represented by
penalised splines. The main idea here is that it may be
useful to represent some relationships in our model by smooth functions
for which the functional form is not pre-specified, but flexibly
estimated from the data. For HMM-like models, this is particularly
valuable, as the latent nature of the state process makes modelling
choices more difficult. For example, choosing an appropriate parametric
family for the state-dependent distributions may be difficult, as we
cannot do state-specific EDA before fitting the model. Also very
difficult is the dependence of transition probabilities on covariates,
as the transitions are not directly observed. Hence, the obvious
alternative is to model these kind of relationships flexibly using
splines but imposing a penalty on the smoothness of the estimated
functions. This leads us to penalised splines.
LaMa contains helper functions that build
design and penalty matrices for given
formulas (using mgcv under the hood) and also functions to
estimate models involving penalised splines in a random effects
framework. For the latter to work, the penalised negative
log-likelihood needs to be compatible with the R package
RTMB to allow for automatic differentiation
(AD). For more information on RTMB, see the
vignette LaMa and RTMB or check out its documentation. For
more information on penalised splines, we recommend Wood (2017).
Smooth transition probabilites
We will start by investigating a 2-state HMM for the
trex data set, containing hourly step lengths and turning
angles of a Tyrannosaurus rex living 66 million years ago. The
transition probabilities are modelled as smooth functions of the time of
day using cyclic P-Splines. The relationship can then
be summarised as
where is a smooth periodic function of time of day. We model the T-rex’s step lengths and turning angles using state-dependent gamma and von Mises distributions.
To ease with model specification, LaMa provides the
function make_matrices() which creates
design and penalty matrices for
regression settings based on the R package mgcv. The user
only needs to specify the right side of a formula using
mgcv syntax and provide data. Here, we use
s(tod, by = "cp") to create the matrices for cyclic
P-splines (cp). This results in a cubic B-Spline basis,
that is wrapped at boundary of the support (0 and 24). We then append
both resulting matrices to the dat list.
library(LaMa)
#> Loading required package: RTMB
head(trex)
#> tod step angle state
#> 1 9 0.3252437 NA 1
#> 2 10 0.2458265 2.234562 1
#> 3 11 0.2173252 -2.262418 1
#> 4 12 0.5114665 -2.958732 1
#> 5 13 0.3828494 1.811840 1
#> 6 14 0.4220099 1.834668 1
modmat = make_matrices(~ s(tod, bs = "cp"), # formula
data = data.frame(tod = 1:24), # data
knots = list(tod = c(0, 24))) # where to wrap the cyclic basis
Z = modmat$Z # spline design matrix
S = modmat$S # penalty matrixWe can now specify the penalised negative log-likelihood
function. We can compute the transition probability matrix the
regular way using tpm_g(). In the last line we need to add
the curvature penalty based on S, which we can conveniently
do using penalty().
pnll = function(par) {
getAll(par, dat)
# cbinding intercept and spline coefs, because intercept is not penalised
Gamma = tpm_g(Z, cbind(beta0, betaSpline))
# computing all periodically stationary distributions for easy access later
Delta = stationary_p(Gamma); REPORT(Delta)
# parameter transformations
mu = exp(logmu); REPORT(mu)
sigma = exp(logsigma); REPORT(sigma)
kappa = exp(logkappa); REPORT(kappa)
# calculating all state-dependent densities
allprobs = matrix(1, nrow = length(step), ncol = N)
ind = which(!is.na(step) & !is.na(angle)) # only for non-NA obs.
for(j in 1:N){
allprobs[ind,j] = dgamma2(step[ind],mu[j],sigma[j]) * dvm(angle[ind],0,kappa[j])
}
-forward_g(Delta[tod[1],], Gamma[,,tod], allprobs) + # regular forward algorithm
penalty(betaSpline, S, lambda) # this does all the penalisation work
}We also have to append a lambda vector to our
dat list which is the initial penalty
strength parameter vector. In this case it is of length two
because our coefficient matrix has two rows.
If you are wondering why lambda is not added to the
par list, this is because for penalised likelihood
estimation, it is a hyperparameter, hence not a true
parameter in the sense of the other parameters in par. One
could, at his point, just use the above penalised likelihood function to
do penalised ML for a fixed penalty strength
lambda.
par = list(logmu = log(c(0.3, 2.5)), # state-dependent mean step
logsigma = log(c(0.2, 1.5)), # state-dependent sd step
logkappa = log(c(0.2, 1.5)), # state-dependent concentration angle
beta0 = c(-2, 2), # state process intercepts
betaSpline = matrix(rep(0, 2*(ncol(Z)-1)), nrow = 2)) # spline coefs
dat = list(step = trex$step, # observed steps
angle = trex$angle, # observed angle
N = 2, # number of states
tod = trex$tod, # time of day (used for indexing)
Z = Z, # spline design matrix
S = S, # penalty matrix
lambda = rep(100, 2)) # initial penalty strengthThe model fit can then be conducted by using the qreml()
function contained in LaMa. The quasi restricted
maximum likelihood algorithm finds a good penalty strength
parameter lambda by treating the spline coefficients as
random effects. Under the hood, qreml() also constructs an
AD function with RTMB but uses the qREML
algorithm (Koslik 2024) to fit the
model. We have to tell the qreml() function which
parameters are spline coefficients by providing the name of the
corresponding list element of par.
There are some rules to follow when using qreml():
The likelihood function needs to be
RTMB-compatible, i.e. have the same structure as the likelihood functions in the vignette LaMa and RTMB. Most importantly, it should be a function of the parameter list only.The penalty strength vector
lambdaneeds its length to correspond to the total number of spline coefficient vectors used. In our case, this is the number of rows ofbetaSpline, but if we additionally had a different spline coefficient (with a different name) in our parameter list, possibly with a different length and a different penalty matrix, we would have needed more elements inlambda.The
penalty()function can only be called once in the likelihood. If several spline coefficients are penalised,penalty()expects a list of coefficient matrices or vectors and a list of penalty matrices. This is shown in the third example in this vignette.When we summarise multiple spline coefficients in a matrix in our parameter list – which is very useful when these are of same lengths and have the same penalty matrix – this matrix must be arranged by row, i.e. each row is one spline coefficient vector. If it is arranged by column,
qreml()will fail.By default,
qreml()assmes that the penalisation hyperparameter in thedatobject is calledlambda. You can use a different name fordat(of course than changing it in yourpnllas well), but if you want to use a different name for the penalisation hyperparameter, you have to specify it as a character string in theqreml()call using thepsnameargument.
system.time(
mod1 <- qreml(pnll, par, dat, random = "betaSpline")
)
#> Creating AD function
#> Initializing with lambda: 100 100
#> outer 1 - lambda: 2.93 2.612
#> outer 2 - lambda: 0.417 0.423
#> outer 3 - lambda: 0.311 0.162
#> outer 4 - lambda: 0.308 0.121
#> outer 5 - lambda: 0.308 0.113
#> outer 6 - lambda: 0.308 0.113
#> Converged
#> Final model fit with lambda: 0.308 0.113
#> user system elapsed
#> 7.483 0.199 7.573The mod object is now a list that contains everything
that is reported by the likelihood function, but also the
RTMB object created in the process. After fitting the
model, we can also use the LaMa function
pred_matrix(), that takes the modmat object we
created earlier, to build a new interpolating design matrix using the
exact same basis expansion specified above. This allows us to plot the
estimated transition probabilities as a smooth function of time of
day.
Gamma = mod1$Gamma
Delta = mod1$Delta
tod_seq = seq(0,24, length = 200)
Z_pred = pred_matrix(modmat, data.frame(tod = tod_seq))
Gamma_plot = tpm_g(Z_pred, mod1$beta) # interpolating transition probs
plot(tod_seq, Gamma_plot[1,2,], type = "l", lwd = 2, ylim = c(0,1),
xlab = "time of day", ylab = "transition probability", bty = "n")
lines(tod_seq, Gamma_plot[2,1,], lwd = 2, lty = 3)
legend("topleft", lwd = 2, lty = c(1,3), bty = "n",
legend = c(expression(gamma[12]^(t)), expression(gamma[21]^(t))))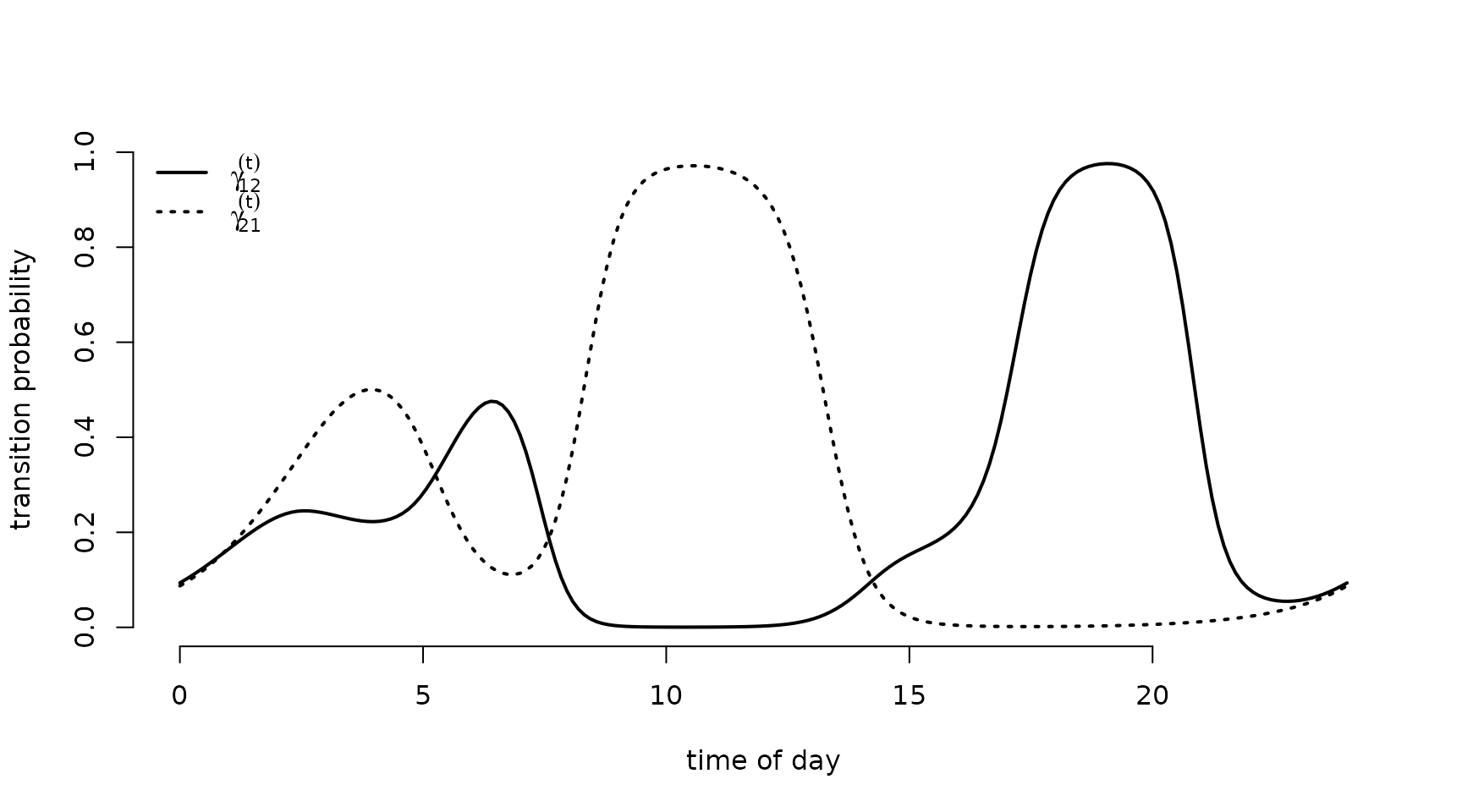
plot(Delta[,2], type = "b", lwd = 2, pch = 16, xlab = "time of day", ylab = "Pr(active)",
col = "deepskyblue", bty = "n", xaxt = "n")
axis(1, at = seq(0,24,by=4), labels = seq(0,24,by=4))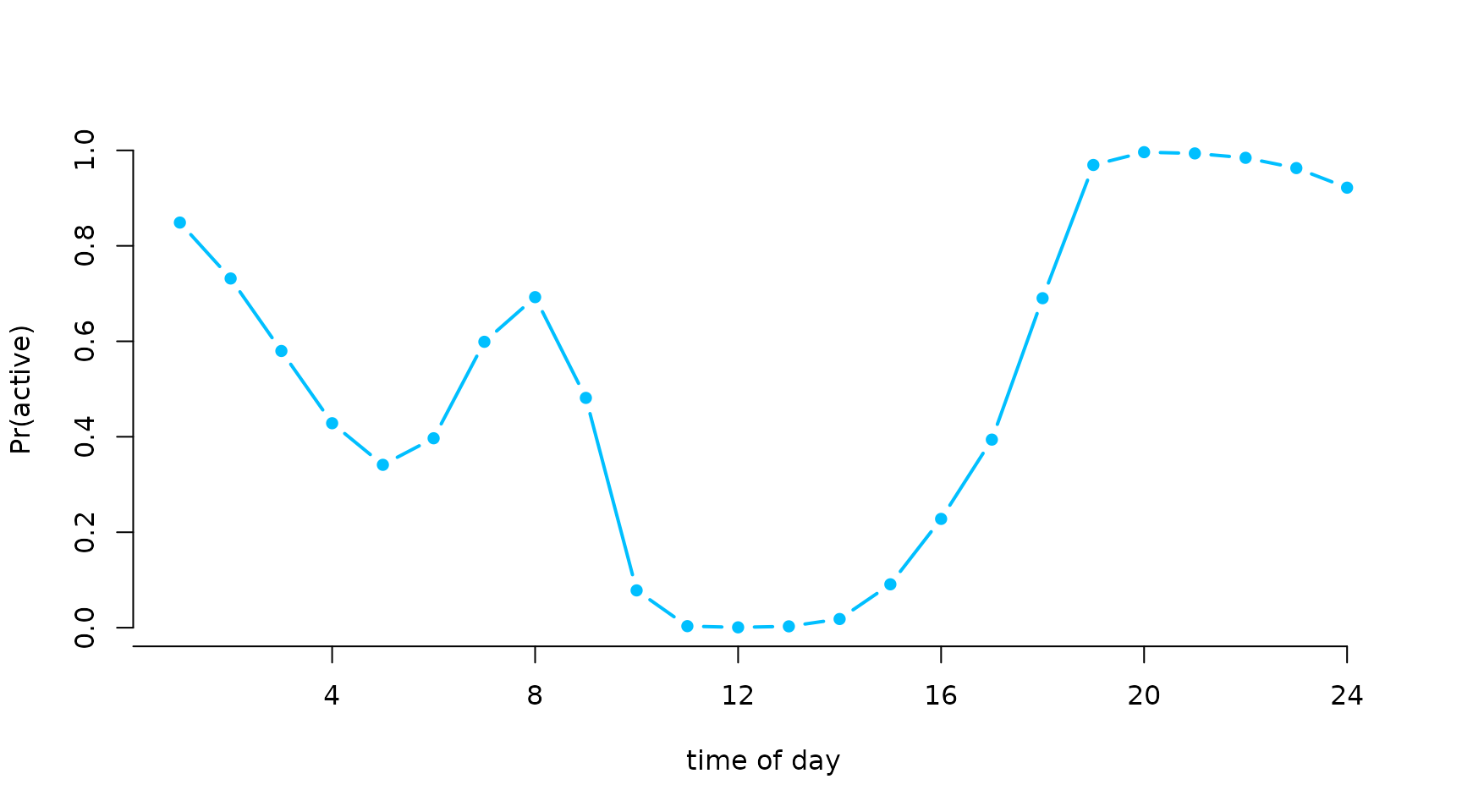
Smooth density estimation
To demonstrate nonparametric estimation of the state-dependent
densities, we will consider the nessi data set. It contains
acceleration data of the Loch Ness Monster, specifically the
overall dynamic body acceleration (ODBA). ODBA is
strictily positive with some very extreme values, making direct analysis
difficult. Hence, for our analysis we consider the logarithm of ODBA as
our observed process.
head(nessi)
#> ODBA logODBA state
#> 1 0.03775025 -3.276763 2
#> 2 0.05417830 -2.915475 2
#> 3 0.03625247 -3.317248 2
#> 4 0.01310802 -4.334531 1
#> 5 0.05402441 -2.918319 3
#> 6 0.06133794 -2.791357 3
hist(nessi$logODBA, prob = TRUE, breaks = 50, bor = "white",
main = "", xlab = "log(ODBA)")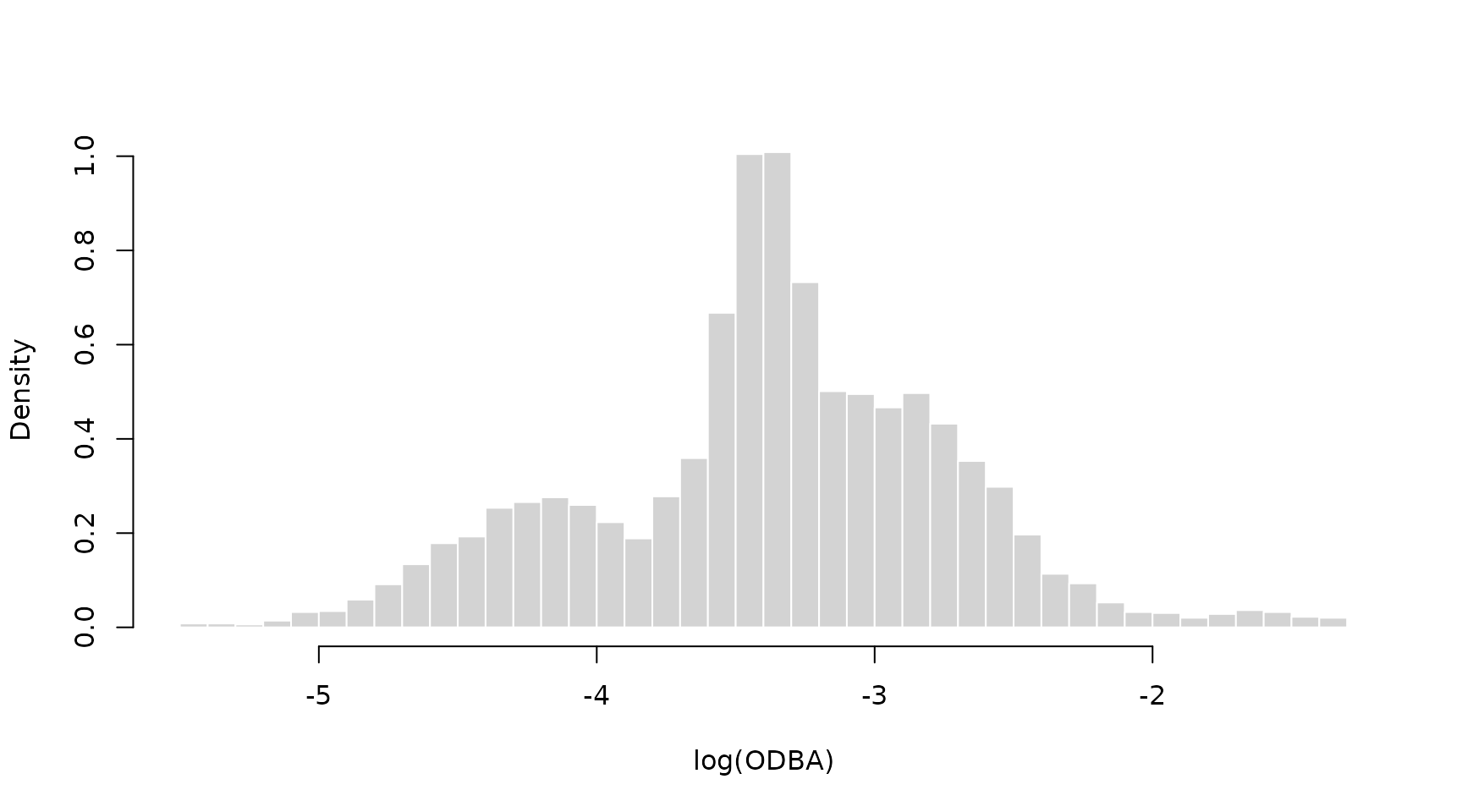
Clearly, there are at least three behavioural states in the data, and we start by fitting a simple 3-state Gaussian HMM with likelihood function:
nll = function(par){
getAll(par, dat)
sigma = exp(logsigma) # exp because strictly positive
REPORT(mu); REPORT(sigma)
Gamma = tpm(eta) # multinomial logit link
delta = stationary(Gamma) # stationary dist of the homogeneous Markov chain
allprobs = matrix(1, length(logODBA), N)
ind = which(!is.na(logODBA))
for(j in 1:N) allprobs[ind,j] = dnorm(logODBA[ind], mu[j], sigma[j])
-forward(delta, Gamma, allprobs)
}We then fit the model as explained in the vignette LaMa and RTMB.
# initial parameter list
par = list(mu = c(-4.5, -3.5, -2.5),
logsigma = log(rep(0.5, 3)),
eta = rep(-2, 6))
# data and hyperparameters
dat = list(logODBA = nessi$logODBA, N = 3)
# creating automatically differentiable objective function
obj = MakeADFun(nll, par, silent = TRUE)
# fitting the model
opt = nlminb(obj$par, obj$fn, obj$gr)
# reporting to get calculated quantities
mod = obj$report()
# visualising the results
color = c("orange", "deepskyblue", "seagreen3")
hist(nessi$logODBA, prob = TRUE, breaks = 50, bor = "white",
main = "", xlab = "log(ODBA)")
for(j in 1:3) curve(mod$delta[j] * dnorm(x, mod$mu[j], mod$sigma[j]),
add = TRUE, col = color[j], lwd = 2, n = 500)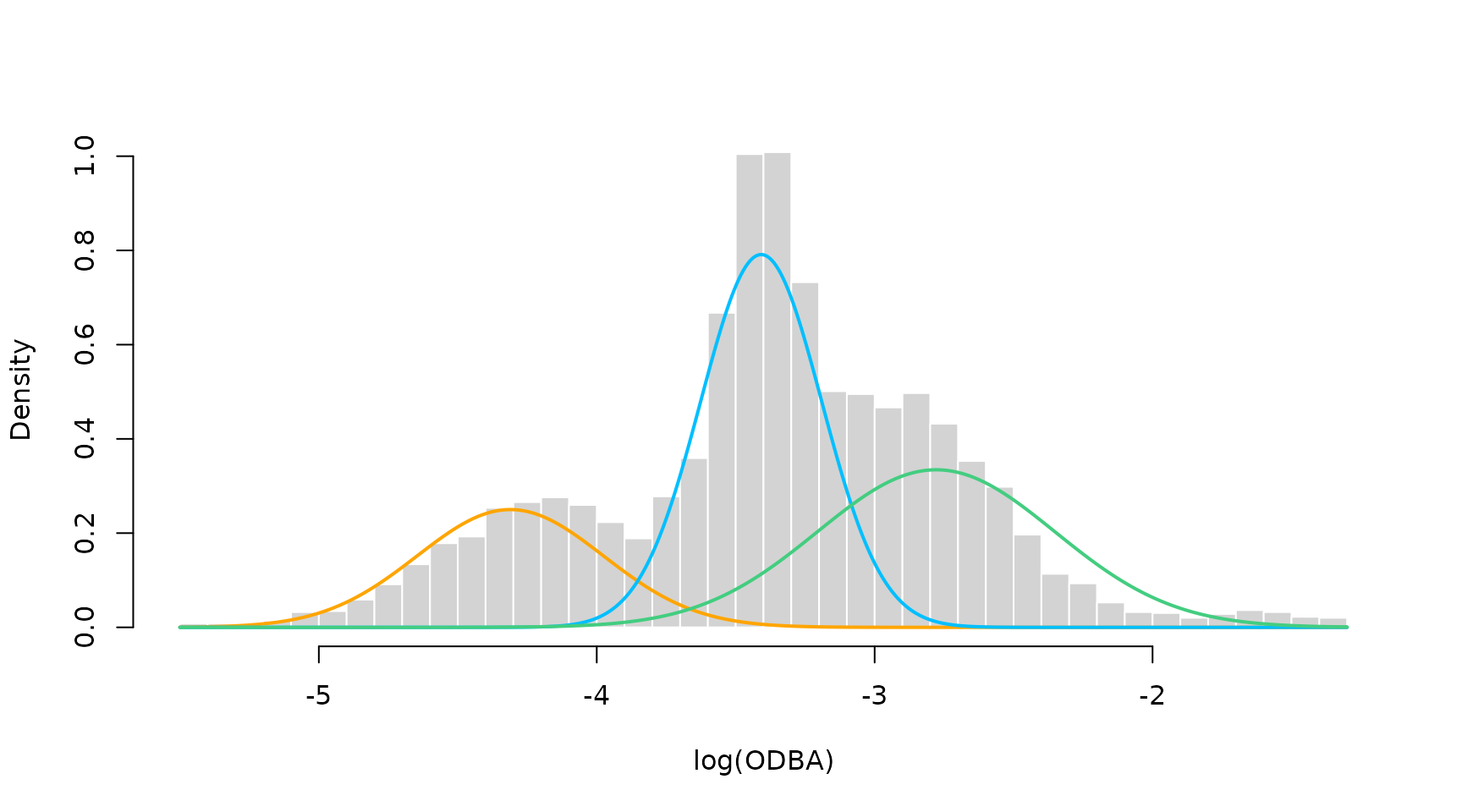
We see a clear lack-of-fit due to the inflexibility of the Gaussian state-dependent densities. Thus, we now fit a model with state-dependent densities based on P-Splines.
In a first step, this requires us to prepare the
design and penalty matrices needed
using buildSmoothDens(). This function can take multiple
data streams and a set of initial parameters (specifying initial means
and standard deviations) for each data stream. It then builds the
P-Spline design and penalty matrices for each data
stream as well as a matrix of initial spline
coefficients based on the provided parameters. The basis
functions are standardised such that they integrate to one, which is
needed for density estimation.
modmat = buildSmoothDens(nessi["logODBA"], # only one data stream here
k = 25, # number of basis functions
par = list(logODBA = list(mean = c(-4, -3.3, -2.8),
sd = c(0.3, 0.2, 0.5))))
#> logODBA
#> Leaving out last column of the penalty matrix, fix the last spline coefficient at zero for identifiability!
#> Parameter matrix excludes the last column. Fix this column at zero!
# par is nested named list: top layer: each data stream
# for each data stream: initial means and standard deviations for each state
# objects for model fitting
Z = modmat$Z$logODBA # spline design matrix for logODBA
S = modmat$S$logODBA # penalty matrix for logODBA
beta = modmat$coef$logODBA # initial spline coefficients
# objects for prediction
Z_pred = modmat$Z_predict$logODBA # prediction design matrix
xseq = modmat$xseq$logODBA # prediction sequence of logODBA valuesThen, we can specify the penalised negative log-likelihood function.
The six lines in the middle are needed for P-Spline-based density
estimation. The coefficient matrix beta provided by
buildSmoothDens() has one column less than the number of
basis functions, which is also printed when calling
buildSmoothDens(). This is because the last column,
i.e. the last coefficient for each state, needs to be fixed to zero for
identifiability which we do by using
cbind(beta, 0). Then, we transform the unconstrained
parameter matrix to non-negative weights that sum to one (called
alpha) for each state using the inverse multinomial
logistic link (softmax). The columnns of the allprobs
matrix are then computed as linear combinations of the columns of
Z and the weights alpha. Lastly, we penalise
the unconstrained coefficients beta (not the constrained
alpha’s) using the penalty() function.
pnll = function(par){
getAll(par, dat)
# regular stationary HMM stuff
Gamma = tpm(eta)
delta = stationary(Gamma)
# smooth state-dependent densities
alpha = exp(cbind(beta, 0))
alpha = alpha / rowSums(alpha) # multinomial logit link
REPORT(alpha)
allprobs = matrix(1, nrow(Z), N)
ind = which(!is.na(Z[,1])) # only for non-NA obs.
allprobs[ind,] = Z[ind,] %*% t(alpha)
# forward algorithm + penalty
-forward(delta, Gamma, allprobs) +
penalty(beta, S, lambda)
}Now we specify the initial parameter and data list and fit the model.
In this case, we actually don’t need to add the observations to our
dat list anymore, as all the information is contained in
the design matrix Z.
par = list(beta = beta, # spline coefficients prepared by buildSmoothDens()
eta = rep(-2, 6)) # initial transition matrix on logit scale
dat = list(N = 3, # number of states
Z = Z, # spline design matrix
S = S, # spline penalty matrix
lambda = rep(10, 3)) # initial penalty strength vector
# fitting the model using qREML
system.time(
mod2 <- qreml(pnll, par, dat, random = "beta")
)
#> Creating AD function
#> Initializing with lambda: 10 10 10
#> outer 1 - lambda: 2.258 1.645 3.555
#> outer 2 - lambda: 1.718 1.411 2.705
#> outer 3 - lambda: 1.627 1.381 2.475
#> outer 4 - lambda: 1.611 1.376 2.401
#> outer 5 - lambda: 1.608 1.375 2.377
#> outer 6 - lambda: 1.608 1.375 2.368
#> outer 7 - lambda: 1.608 1.375 2.367
#> outer 8 - lambda: 1.608 1.375 2.367
#> Converged
#> Final model fit with lambda: 1.608 1.375 2.367
#> user system elapsed
#> 19.256 2.703 18.597After fitting the model, we can easily visualise the smooth densities
using the prepared prediction objects. We already have access to all
reported quanitites because qreml() automatically runs the
reporting after model fitting.
sDens = Z_pred %*% t(mod2$alpha) # all three state-dependent densities on a grid
hist(nessi$logODBA, prob = TRUE, breaks = 50, bor = "white", main = "", xlab = "log(ODBA)")
for(j in 1:3) lines(xseq, mod2$delta[j] * sDens[,j], col = color[j], lwd = 2)
lines(xseq, colSums(mod2$delta * t(sDens)), col = "black", lwd = 2, lty = 2)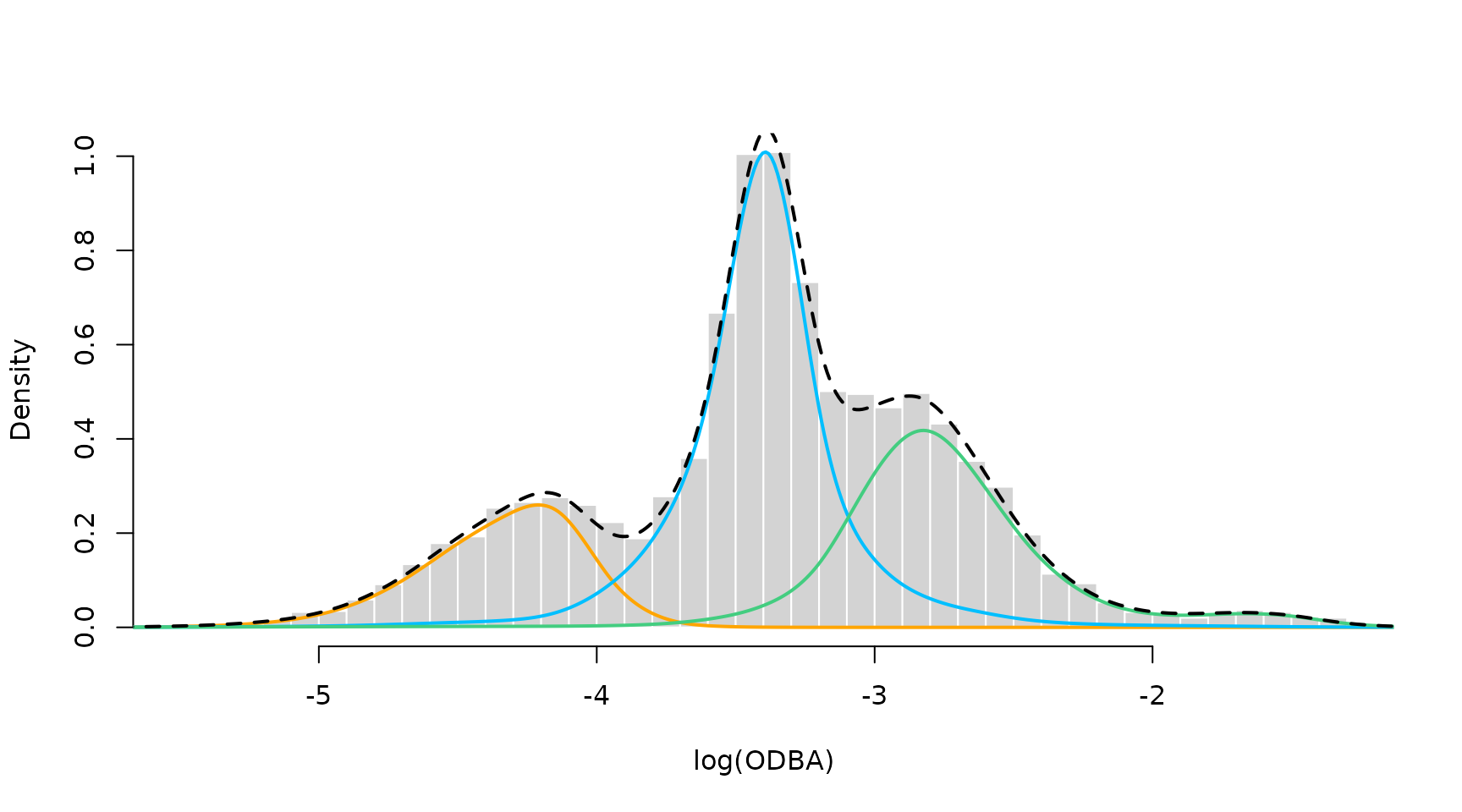
The P-Spline model results in a very good fit to the empirical distribution. This is beause the first state has a skewed distribution, the second state has a high kurtosis and the third state has a funny right tail. The P-Spline model can capture all of these features where the parametric model failed to do so.
Markov-switching GAMLSS
Lastly, we want to demonstrate how one can easily fit
Markov-switching regression models where the state-dependent means and
potentially other parameters depend on covariates via smooth functions.
For this, we consider the energy data set contained in the
R package MSwM. It comprises 1784 daily observations of
energy prices (in Cents per kWh) in Spain which we want to explain using
the daily oil prices (in Euros per barrel) also provided in the data.
Specifically, we consider a 2-state MS-GAMLSS defined by
not covering other potential
explanatory covariates for the sake of simplicity.
data(energy, package = "MSwM")
head(energy)
#> Price Oil Gas Coal EurDol Ibex35 Demand
#> 1 3.188083 22.43277 14.40099 38.35157 1.134687 8.3976 477.3856
#> 2 4.953667 22.27263 19.02747 38.35157 1.106439 8.3771 609.1261
#> 3 4.730917 22.65383 18.48417 38.35157 1.106684 8.5547 650.3715
#> 4 4.531000 23.67657 18.30143 38.35157 1.116819 8.4631 647.0499
#> 5 5.141875 23.67209 14.55602 38.35157 1.122965 8.1773 627.9698
#> 6 6.322083 23.60534 15.22485 38.35157 1.122460 8.1866 693.2467Similar to the first example, we can prepare the model matrices using
make_matrices():
modmat = make_matrices(~ s(Oil, k = 12, bs = "ps"), energy)
Z = modmat$Z # design matrix
S = modmat$S # penalty matrix (list)Then, we specify the penalised negative log-likelihood function. It
differs from the first example as the state-dependent distributions, as
opposed to the state process parameters, depend on the covariate.
Additionally, we now have two completely separated spline-coefficient
matrices/ random effects called betaSpline and
alphaSpline for the state-dependent means and standard
deviations respectively. Thus, we need to pass them as a list to the
penalty() function.
We also pass the penalty matrix list S that is provided
by make_matrices(). This could potentially be a list of
length two if the two spline coefficient matrices were penalised
differently (e.g. by us using a different spline basis). In this case,
however, they are the same and we only pass the list of length one. It
does not matter to penalty() if we pass a list of length
one or just one matrix.
pnll = function(par) {
getAll(par, dat)
Gamma = tpm(eta) # computing the tpm
delta = stationary(Gamma) # stationary distribution
# regression parameters for mean and sd
beta = cbind(beta0, betaSpline); REPORT(beta) # mean parameter matrix
alpha = cbind(alpha0, alphaSpline); REPORT(alpha) # sd parameter matrix
# calculating all covariate-dependent means and sds
Mu = Z %*% t(beta) # mean
Sigma = exp(Z %*% t(alpha)) # sd
allprobs = cbind(dnorm(price, Mu[,1], Sigma[,1]),
dnorm(price, Mu[,2], Sigma[,2])) # state-dependent densities
- forward(delta, Gamma, allprobs) +
penalty(list(betaSpline, alphaSpline), S, lambda)
}From this point on, the model fit is now basically identical to the
previous two examples. We specify initial parameters and include an
inital penalty strength parameter in the dat list.
# initial parameter list
par = list(eta = rep(-4, 2), # state process intercepts
beta0 = c(2, 5), # state-dependent mean intercepts
betaSpline = matrix(0, nrow = 2, ncol = 11), # mean spline coef
alpha0 = c(0, 0), # state-dependent sd intercepts
alphaSpline = matrix(0, nrow = 2, ncol = 11)) # sd spline coef
# data, model matrices and initial penalty strength
dat = list(price = energy$Price,
Z = Z,
S = S,
lambda = rep(1e3, 4))
# model fit
system.time(
mod3 <- qreml(pnll, par, dat, random = c("betaSpline", "alphaSpline"))
)
#> Creating AD function
#> Initializing with lambda: 1000 1000 1000 1000
#> outer 1 - lambda: 238.423 106.067 189.083 42.362
#> outer 2 - lambda: 70.263 17.577 55.015 7.935
#> outer 3 - lambda: 36.315 8.566 26.41 4.88
#> outer 4 - lambda: 27.185 7.426 15.297 4.336
#> outer 5 - lambda: 24.236 7.257 10.88 4.214
#> outer 6 - lambda: 23.193 7.225 9.211 4.182
#> outer 7 - lambda: 22.808 7.217 8.602 4.173
#> outer 8 - lambda: 22.661 7.215 8.384 4.17
#> outer 9 - lambda: 22.593 7.212 8.306 4.169
#> outer 10 - lambda: 22.578 7.213 8.278 4.168
#> outer 11 - lambda: 22.575 7.212 8.276 4.168
#> outer 12 - lambda: 22.575 7.212 8.276 4.168
#> Converged
#> Final model fit with lambda: 22.575 7.212 8.276 4.168
#> user system elapsed
#> 7.528 3.541 6.787Having fitted the model, we can visualise the results. We first
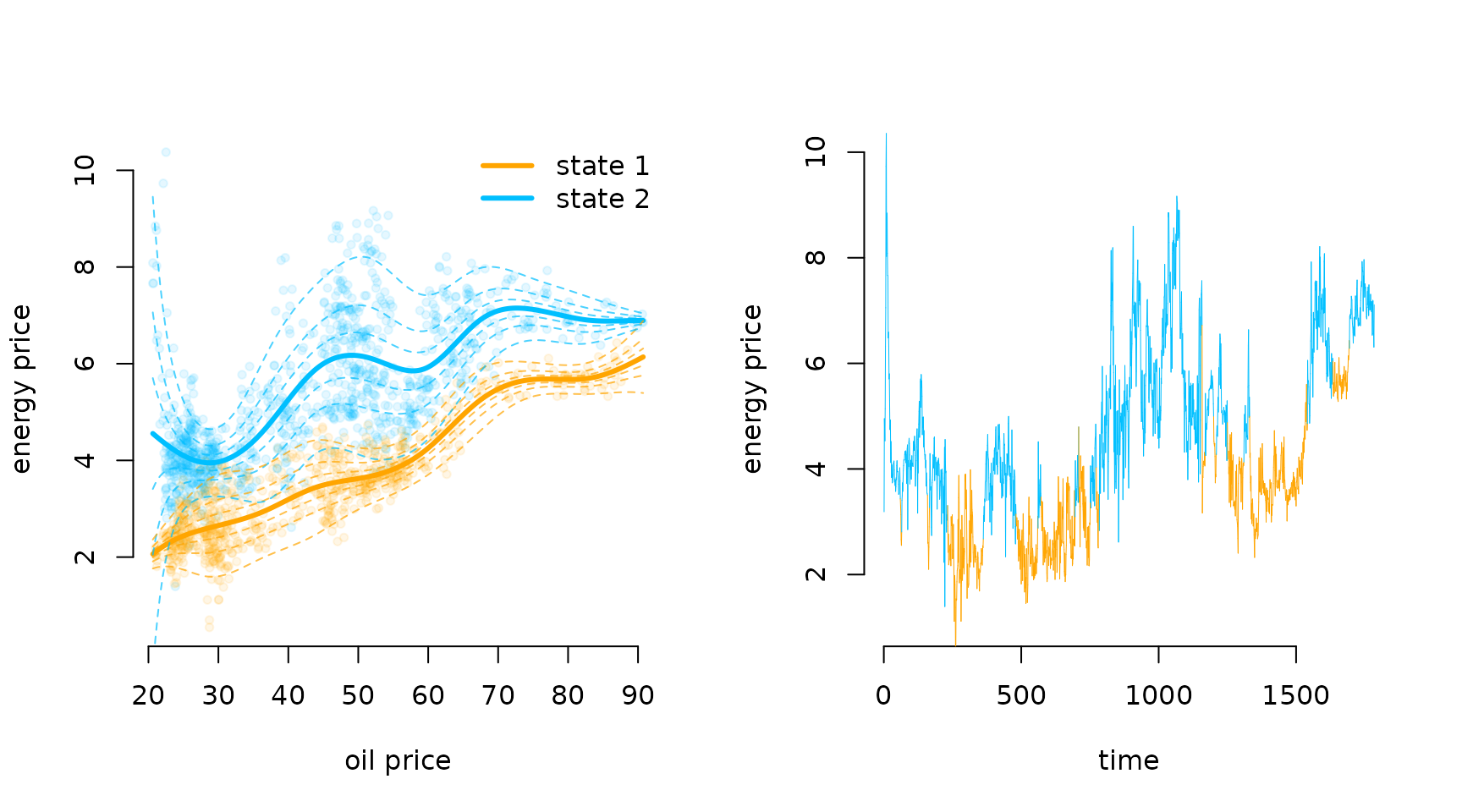
decode the most probable state sequence and then plot the estimated
state-dependent densities as a function of the oil price, as well as the
decoded time series. For the former, we create a fine grid of oil price
values and use the pred_matrix() function to build the
associated interpolating design matrix.
xseq = seq(min(energy$Oil), max(energy$Oil), length = 200) # sequence for prediction
Z_pred = pred_matrix(modmat, newdata = data.frame(Oil = xseq)) # prediction design matrix
mod3$states = viterbi(mod3$delta, mod3$Gamma, mod3$allprobs) # decoding most probable state sequence
Mu_plot = Z_pred %*% t(mod3$beta)
Sigma_plot = exp(Z_pred %*% t(mod3$alpha))
library(scales) # to make colors semi-transparent
par(mfrow = c(1,2))
# state-dependent distribution as a function of oil price
plot(energy$Oil, energy$Price, pch = 20, bty = "n", col = alpha(color[mod3$states], 0.1),
xlab = "oil price", ylab = "energy price")
for(j in 1:2) lines(xseq, Mu_plot[,j], col = color[j], lwd = 3) # means
qseq = qnorm(seq(0.5, 0.95, length = 4)) # sequence of quantiles
for(i in qseq){ for(j in 1:2){
lines(xseq, Mu_plot[,j] + i * Sigma_plot[,j], col = alpha(color[j], 0.7), lty = 2)
lines(xseq, Mu_plot[,j] - i * Sigma_plot[,j], col = alpha(color[j], 0.7), lty = 2)
}}
legend("topright", bty = "n", legend = paste("state", 1:2), col = color, lwd = 3)
# decoded time series
plot(NA, xlim = c(0, nrow(energy)), ylim = c(1,10), bty = "n",
xlab = "time", ylab = "energy price")
segments(x0 = 1:(nrow(energy)-1), x1 = 2:nrow(energy),
y0 = energy$Price[-nrow(energy)], y1 = energy$Price[-1],
col = color[mod3$states[-1]], lwd = 0.5)